ALDS 1. Sparse Table
Migrated
This article is migrated from which I wrote on another website.
안녕하세요. 이번 시리즈에서는 유용한 알고리즘과 자료구조를 몇 가지 다루어보고자 합니다. 이 시리즈의 첫 번째 타겟으로는 Sparse Table을 다뤄보겠습니다.
이 포스팅은 cp-algorithms를 참고하였음을 알려드립니다.
What is sparse table?¶
Sparse Table은 Range Query를 답변할 수 있게 해주는 자료구조입니다. (하지만 Segment Tree와는 구조가 좀 다른데, 뒷 문단에서 설명드리겠습니다.)
Pre-condition¶
- Sparse Table에서 다루는 연산은 결합 법칙을 만족해야 합니다.
- Sparse Table에서 \(O(1)\) 수준의 쿼리를 위해서는 "겹쳐짐 허용(?)"을 만족해야 합니다.
Structure¶
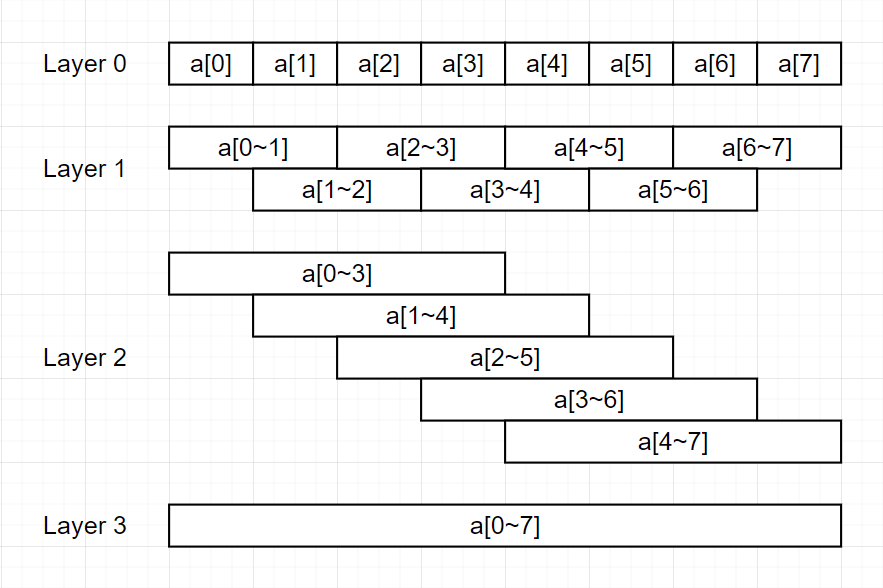
Sparse Table의 특징은, 임의의 시작점과 임의의 2의 거듭제곱 길이의 구간에 대한 operation의 결과물을 모조리 저장하는 것입니다. 다음 그림은 길이가 8인 배열을 가지고 Sparse Table을 만드는 예시입니다.
- Layer \(0\)은 원래 배열과 동일한 구조를 이룹니다.
- Layer \(n\) (\(n > 0\))은 Layer \(n-1\)보다 길이가 2배인 임의의 구간을 모아놓은 것입니다.
Pre-calculation¶
총 구간의 개수는 \(O \Bigl((n - 1 + 1) + (n - 2 + 1) + (n - 4 + 1) + \cdots + (n - \log{n} + 1) \Bigr) \sim O(n \log n)\) 개이고, Layer 0을 제외한 임의의 Layer는 하위 Layer의 2개의 구간의 정보를 이용하여 \(O(1)\)에 연산을 구할 수 있으므로(ex: \(\min(a[0, 1], a[2, 3]) = a[0, 3]\)), 모든 Layer의 모든 구간의 값을 구하는 데(전처리) 총 \(O(n \log{n})\)의 시간이 소모됩니다.
Querying¶
Sparse Table이 진가를 발휘하는 부분이 바로 이 부분입니다. Min, Max 같이 두 피연산자 구간에 서로 겹치는 영역이 있더라도 상관이 없는 연산(ex: \(\min(a[1,4], a[2,5]) = a[1,5]\))을 다룰 때 특히 유용합니다.
어떤 연산 \(\oplus\)에 대해, 해당 연산이 결합 법칙을 만족하고, \((\bigoplus_{i=l_1}^{l_2} a[i]) \oplus (\bigoplus_{i=l_3}^{l_4} a[i]) = \bigoplus_{i=l_1}^{l_4} a[i]\) (\(l_1 \le l_3 \le l_2 \le l_4\))를 만족한다고 합시다.
그렇다면, \(\bigoplus_{i=l}^{r} a[i] = (\bigoplus_{i=l}^{l+2^k-1} a[i]) \oplus (\bigoplus_{i=r-2^k+1}^{r} a[i])\)인 \(k\)가 무조건 존재합니다! 따라서, 해당 \(k\)를 찾기만 한다면 Querying을 \(O(1)\)에 할 수 있습니다. 일반적으로 \(k\)는 커봐야 몇십 정도의 작은 정수이고, 대부분의 경우 그런 \(k\)를 찾을 수 있는 매우 빠른 함수(__builtin_clz, bit_width 등)를 활용할 수 있으므로, 쿼리 속도가 매우 빠릅니다!
Code¶
윗 문단에서의 설명은 모든 range가 inclusive하지만 코드 내 range는 start-inclusive, end-exclusive함에 유의해주시기 바랍니다.
class SparseTable{
protected: // Properties
int n;
std::vector<std::vector<lld>> feature_min, feature_max;
// Constructor
public: SparseTable(const std::vector<lld> &base){
n = (int)base.size();
int log = 0;
while((1<<log) < (int)base.size()) log++;
log++;
// Feature initialization
feature_min.clear(); feature_min.resize(log, std::vector<lld>(n, inf));
feature_min[0] = base;
feature_max.clear(); feature_max.resize(log, std::vector<lld>(n, -inf));
feature_max[0] = base;
initialize();
}
// Initialize base feature.
private: void initialize(){
// feature[level][offset] =
// operation(base[offset : offset + 2 ** level])
for(int log=1; log < (int)feature_min.size(); log++){
int halflen = 1 << (log-1);
for(int offset=0; offset + halflen < n; offset++){
feature_min[log][offset] = std::min(
feature_min[log-1][offset],
feature_min[log-1][offset + halflen]
);
feature_max[log][offset] = std::max(
feature_max[log-1][offset],
feature_max[log-1][offset + halflen]
);
}
}
}
// Return min[left:right], max[left:right]
public: std::pair<lld, lld> query(int left, int right){
if(left >= right) return {inf, -inf};
int log = 0;
while((1 << log) < right - left) log++;
if(log) log--;
lld min = std::min(
feature_min[log][left],
feature_min[log][right - (1<<log)]
);
lld max = std::max(
feature_max[log][left],
feature_max[log][right - (1<<log)]
);
return {min, max};
}
};
이상으로 ALDS 시리즈의 첫 번째 포스팅을 마치겠습니다. 읽어주셔서 감사합니다.