ALDS 6. Concatenation Equality Problem
안녕하세요. 이번 게시글에서는 Github 갤러리 2025년 신년맞이 문제를 알고리즘적으로 해결하는 방법에 대해 서술해보고자 합니다. 알고리즘을 놓은 지는 꽤 오래 되어서, 오랜만의 각 잡고 문제를 푸는 과정이 재밌게 느껴졌네요.
Statement¶
문자열 \(x\)와 \(y\)에 대해, \(x+y\)를 \(x\)와 \(y\)의 concatenation으로 정의합니다.
예를 들어, "abcd" + "efgh"는 "abcdefgh"입니다.
유한개 문자열의 목록 \(s_1, s_2, \ldots, s_n\)이 주어졌을 때, 임의의 \(i\), \(j\)에 대하여 \(s_i + s_j = s_j + s_i\)인지 확인해주세요. (\(n \ge 2\), 원문에서는 \(i < j\)인 경우만 따지지만, 실제로는 \(i = j\)인 경우까지 따져도 참/거짓에 변함이 없습니다.)
Example 1¶
답은 참입니다.
Example 2¶
답은 거짓입니다.
(반례: "abc" + "abcd" != "abcd" + "abc")
Base case¶
먼저 두 문자열 \(x\)와 \(y\)의 길이가 같을 때 \(x+y = y+x\)가 되려면 어떤 조건을 만족해야 하는지부터 알아봅시다. 상당히 직관적인데, 결론부터 말하면 \(x\)와 \(y\)가 동일한 문자열이면 됩니다.
| Index | \(0\) | \(1\) | \(\cdots\) | \(n-2\) | \(n-1\) | \(n\) | \(n+1\) | \(\cdots\) | \(2n-2\) | \(2n-1\) |
|---|---|---|---|---|---|---|---|---|---|---|
| \(x+y\) | \(x_0\) | \(x_1\) | \(\cdots\) | \(x_{n-2}\) | \(x_{n-1}\) | \(y_0\) | \(y_1\) | \(\cdots\) | \(y_{n-2}\) | \(y_{n-1}\) |
| \(y+x\) | \(y_0\) | \(y_1\) | \(\cdots\) | \(y_{n-2}\) | \(y_{n-1}\) | \(x_0\) | \(x_1\) | \(\cdots\) | \(x_{n-2}\) | \(x_{n-1}\) |
이 그림에서 \(x_i\)와 \(y_i\)는 각각 \(x\)와 \(y\)의 \(i\)번째 인덱스에 있는 글자입니다. (0-based) \(x+y = y+x\)이기 위해서는 \(x_0 = y_0\) , \(x_1 = y_1\) , \(\cdots\) 여야 하는데, 이 조건은 \(x=y\)와 일치합니다. 역도 성립하므로, \(x\)와 \(y\)의 길이가 같으면 \(x+y = y+x\)와 \(x=y\)는 동치입니다.
Length-multiple case¶
이번에는 \(x\)의 길이가 \(y\)의 길이의 정수배일때 어떤 조건을 만족해야 하는지 알아봅시다. (아래 표에서 \(c = |y|\) 입니다.)
| Index range | \([0, c)\) | \([c, 2c)\) | \([2c, 3c)\) | \(\cdots\) | \([(n-1)c, nc)\) | \([nc, (n+1)c)\) |
|---|---|---|---|---|---|---|
| \(x+y\) | \(x_{0 \cdots c}\) | \(x_{c \cdots 2c}\) | \(x_{2c \cdots 3c}\) | \(\cdots\) | \(x_{(n-1)c \cdots nc}\) | \(y\) |
| \(y+x\) | \(y\) | \(x_{0 \cdots c}\) | \(x_{c \cdots 2c}\) | \(\cdots\) | \(x_{(n-2)c \cdots (n-1)c}\) | \(x_{(n-1)c \cdots nc}\) |
\(x+y = y+x\)이기 때문에 \(x_{0 \cdots c} = x_{(n-1)c \cdots nc} = y\)가 되고, 동시에 \(x_{0 \cdots c} = x_{c \cdots 2c} = x_{2c \cdots 3c} = \cdots\) 이므로, \(x\)는 \(y\)를 \(n\)번 반복한 문자열이 됩니다.
Formal하게 다시 말하면, \(x\)의 길이가 \(y\)의 길이의 정수배일때, \(x+y = y+x\)가 되기 위해서는 \(x = y + y + \cdots + y\) (\(n\)개의 \(y\)의 합)이 되어야 합니다.
General case¶
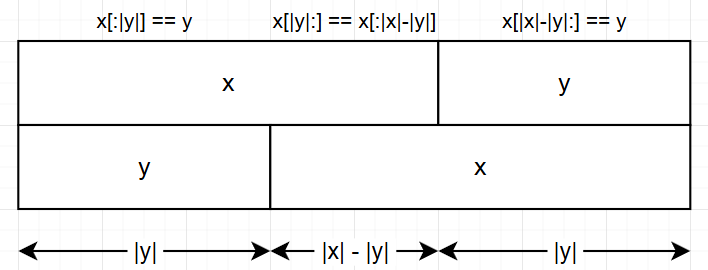
이제 두 문자열의 길이가 다른 케이스에 대해 알아보겠습니다. 일반성을 잃지 않고 \(x\)의 길이가 \(y\)보다 크다고 가정해보겠습니다.
여기서 알 수 있는 사실은, \(x_{0\ldots |y|} = x_{|x| - |y| \ldots |x|}\) 이면서 동시에 \(x_{|y| \ldots |x|} = x_{0 \ldots |x| - |y|}\)라는 것입니다. (End exclusive입니다.) 이제 다음 그림을 봅시다.
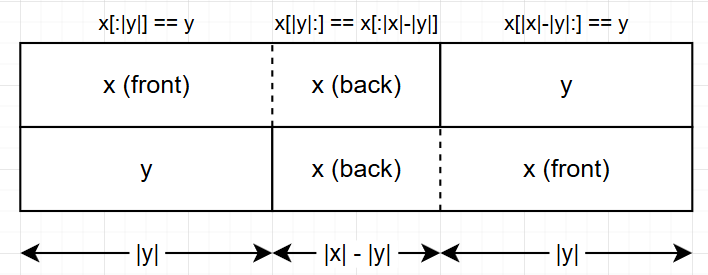
이게 뭘 의미하냐면, \(x + y = y + x\) 일 경우, \(x_{front} + x_{back} = x_{back} + x_{front}\)가 성립한다는 것입니다. (\(y = x_{front}\) , \(x = x_{front} + x_{back}\)) 이 명제의 역도 성립할까요?
이고, 동시에
이므로 역도 성립합니다. 따라서 둘은 동치입니다.
그래서 우리는 \(x_{front} + x_{back} = x_{back} + x_{front}\) 인지만 보면 됩니다. 그리고 우리는 여기서 유클리드 호제법의 아이디어를 접근할 것입니다.
Euclidean algorithm¶
유클리드 호제법이란, 두 정수 \(a\)와 \(b\)의 최대공약수(gcd)를 \(\log{(\max(a,b))}\)에 구하는 알고리즘입니다. 이 알고리즘의 기초가 되는 식은 다음과 같습니다.
예를 들어서,
이런 식으로 \(12\)와 \(7\)의 최대공약수가 \(1\)임을 알 수 있습니다. 이제 이 알고리즘을 염두에 두고 위 그림을 다시 쳐다보면.. 뭔가 느껴지실 겁니다.
Quote
"아! 이거 재귀적으로 들어갈 수 있구나."
그렇습니다. 이제 우리는 일반적인 모든 경우를 풀 수 있습니다.
The final phase¶
저희는 위에서 다음과 같은 수식을 유도했습니다.
그리고 이제 이 수식을 다음과 같은 느낌으로 표현할 수 있습니다.
어떤 문자열 \(x + y = s\)에 대해, \(f(s, |x|, |y|)\)를 주어진 문제의 정답이라고 표현해봅시다. 이 값은 true 또는 false이며, \(s_{0 \ldots |x|}\)와 \(s_{|x| \ldots |x|+|y|}\)가 서로 교환되는지 유무를 뜻합니다.
이것이 의미하는 바는 \(x+y = y+x\) 이기 위해서는, \(x\)와 \(y\)가 각각 어떤 공통 문자열의 정수배 반복이어야 한다는 것입니다.
이걸 \(2\)개 문자열이 아니라 \(n\)개 문자열에 대해 확장하는 것도 동일한 원리에 의해 가능합니다.
그래서 원래 문제를 풀기 위해서는, 먼저 \(g = gcd(|s_1|, |s_2|, \ldots, |s_n|)\)을 구한 뒤, 각 문자열이 첫 \(g\)개 글자에 해당하는 문자열의 반복인지를 확인하면 됩니다. 그래서 이 문제는 시간복잡도 \(O(|s_1| + |s_2| + \ldots + |s_n|)\)에 풀 수 있습니다.
오랜만에 알고리즘 문제를 푸니까 재미있네요. 글을 읽어주셔서 감사합니다.