Skip to content

ALDS 7. Implementing Poker Analysis Library (Algorithm Part)

안녕하세요.

이번에는 포커 토너먼트 분석툴을 만들어본 경험을 풀어보려고 합니다. 제 포커 토너먼트 분석툴은 GGNetwork의 Pokercraft에서 다운로드 받을 수 있는 데이터를 분석하는 툴로, 그 툴로 만든 분석파일들은 다음과 같습니다.

취미 프로젝트 치고는 코딩을 꽤 많이 한 편이라, 글로 풀어보고 싶었습니다. 이 글에서는 그 중 수학/알고리즘적 부분과 연관이 있는 부분만 골라서 풀어보겠습니다.

Monte-Carlo analysis

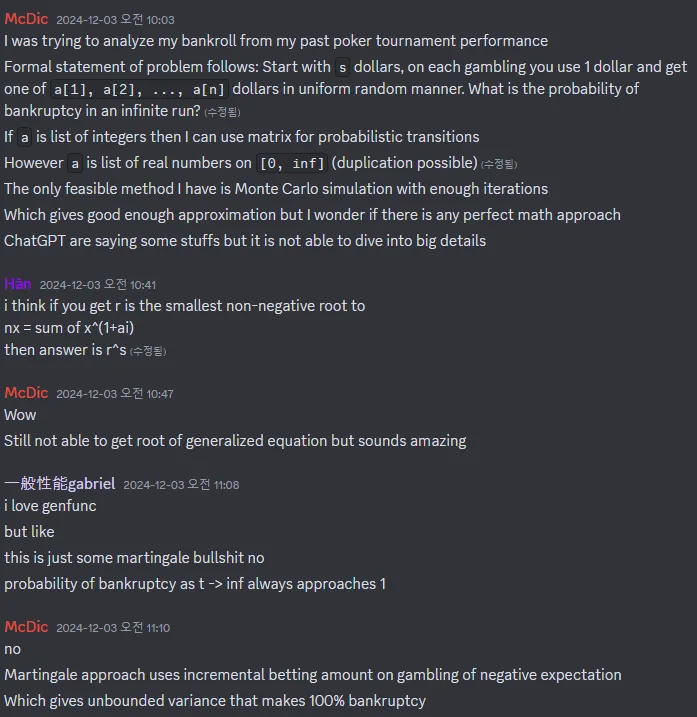
\(i\)번째 도박에서 1달러를 투자했는데 얻은 금액을 \(p_i\)라고 합시다. \(p_1, p_2, \ldots, p_n\) 데이터를 가지고 있을 때, \(s\)달러를 들고 이 도박을 장기적으로 계속 한다면, 중간에 파산하지 않고 무한히 돈을 벌 수 있는 확률은 얼마일까요?

저는 이 문제를 수학적으로 완전하게 접근할 방법을 찾지 못했습니다. 하지만 다행인 점은 이런 식으로 정확한 값을 계산하기 어려운 문제를 랜덤 시뮬레이션으로 풀어낼 방법이 있다는 것입니다. 저는 Monte Carlo 시뮬레이션을 통해서 근사값을 구하는 것으로 적당히 퉁쳤습니다.

talk

Formula

수학적으로 엄밀하게 접근하면,

\[f(x) = \sum_{i} (x^{(1 + p_i)} - x)\]

의 가장 작은 양수 근을 \(r\)이라고 할 때, 파산 확률은 \(r^s\) 라고 합니다. (실제 데이터에서는 \(p_i = 0\)인 \(i\)가 있으므로, 답이 \(0\)이 될 수는 없습니다) 여전히 해당 방정식을 엄밀하게 풀어낼 방법은 생각나지 않지만.. 신기하네요.

Luck score computation

\(i\)번째 올인에서 이기는 확률변수를 \(win_i\)라고 정의하면,

\[W = \sum_{i} \Bbb1[\mathrm{win}_i]\]

로 정의된 \(W\)가 Poisson-Binomial 분포를 따르게 됩니다. 저는 여기서 tail probability (\(\mathrm{Pr}(W \le w_{obs})\))를 구하고, 그 값을 다시 Guassian quantile function에 집어넣기로 했습니다. Tail probability를 구하기 위해 계산해야 하는 Poisson Binomial의 PDF는 DP를 통해 구할 수 있고, 점화식은 다음과 같습니다.

\[ f_{i}[k] = f_{i-1}[k](1 - p_i) + f_{i-1}[k-1] p_i \space (\forall_{x > 0} \space f_{0}[x] = 0, \space f_0[0] = 1) \]

위 점화식을 \(i = 1, 2, 3, \ldots\)에 대해 반복하면 최종 \(f_n\) 결과가 PDF가 됩니다. 이 점화식의 시간복잡도는 \(O(n^2)\)인데, 2차원으로 펼쳐보시면 느끼시겠지만 파스칼의 삼각형과 양상이 매우 유사합니다. 차이점이라면 매 층마다 propagation weight가 left parent, right parent가 1:1이 아니고 \(1 - p_i, p_i\) 입니다. 그래서 이 점화식을 polynomial multiplication으로 생각하면 FFT를 활용하여 성능을 높일 수 있습니다.

\[ \begin{aligned} f_{i} &= f_{i-1} \cdot (p_i x + 1 - p_i) \\ f_n &= \prod_i (p_i x + 1 - p_i) \end{aligned} \]

이제 이것은 \(n\)개의 다항식을 곱하는 문제로 바뀌었고, FFT로 최적화하면 됩니다.

다른 파트들은 다음 글에서 읽으실 수 있습니다.

글을 읽어주셔서 감사합니다.