Skip to content

POKER 9. Meaningless Trial on Lottery

로또에 관하여 생각하다가, 문득 다음과 같은 아이디어가 생각났습니다.

Quote

로또를 자동으로 사지 말고, 수동으로 서로 번호가 안 겹치게 사면, 높은 등수가 나올 확률 혹은 투자 대비 리턴이 조금이라도 올라가지 않을까?

물론 로또는 배당률이 50%이고 대부분의 배당금이 1등에게 할당되어 있기 때문에 그렇게 유의미한 수익을 얻긴 어려울 거라 생각했으나, 일단 머릿속에 생각난 김에 Rust를 사용하는 회사 입사를 앞두고 있는 겸, 리서치 코딩을 시작해보았습니다.

How Korean lottery works

대한민국의 로또는 몇 안 되는 합법적인들 도박 중 하나로, "(주)동행복권"에서 운영하고 있는 복권사업입니다. 동행복권은 제주반도체, 쌍용정보통신, FASOO, NHN클라우드, 케이뱅크 등이 주주로 있는, 기획재정부가 지정한 복권 수탁사업자입니다.

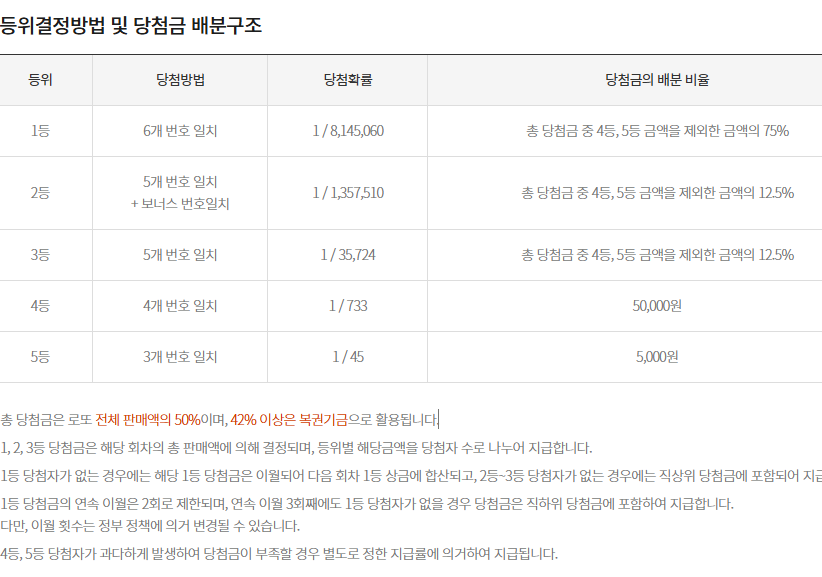
동행복권에서 운영하는 복권 중 가장 규모가 큰 "로또 6/45"는, 45개 번호 중에서 6개를 뽑아 당첨을 가리는 복권입니다.

official_website

Caption

로또 6/45에서는 6개의 번호와 1개의 보너스 번호를 뽑습니다. 당첨 방법은 이미지에 써진 것과 같고, 실제 당첨확률은 웹사이트에 써진 것과 살짝 다른데, 다음과 같습니다.

등수 당첨되는 번호의 수 당첨확률 당첨시 기대 상금 기대값
1등 \(1\) 1 / 8,145,060 1,952,160,000원 0.23967
2등 \(6 = \binom{6}{5}\) 1 / 1,357,510 54,226,666원 0.03995
3등 \(228 = \binom{6}{5} \times (45 - 6 - 1)\) 1 / 35,723.95 1,427,017원 0.03995
4등 \(11115 = \binom{6}{4} \times \binom{45-6}{2}\) 1 / 732.79892 50,000원 (고정) 0.06823
5등 \(182780 = \binom{6}{3} \times \binom{45-6}{3}\) 1 / 44.562097 5,000원 (고정) 0.11220

Formula

위 기대값과 당첨확률은 다음 코드를 기반으로 계산되었습니다.

/// This function calculates `C(n, r)`.
/// Warning: This function will result overflow for large numbers.
pub const fn binomial(n: u64, r: u64) -> u64 {
    if r == 0 || r == n || n == 1 {
        1
    } else {
        binomial(n - 1, r - 1) * n / r
    }
}

const LOTTERY_CASES: [u64; 6] = [
    0,
    1,
    binomial(6, 5),
    binomial(6, 5) * binomial(38, 1), // 228
    binomial(6, 4) * binomial(39, 2), // 11115
    binomial(6, 3) * binomial(39, 3), // 182780
];

/// Get lottery rank return for 45/6 lottery.
const fn get_lottery_rank_return(rank: usize) -> f64 {
    const TOTAL_CASES: u64 = binomial(45, 6); // 8145060
    const HIGH_RETURN_RATIO: [f64; 4] = [0.0, 0.75, 0.125, 0.125];
    const LOW_RETURN_RATIO: [u64; 6] = [0, 0, 0, 0, 50, 5];
    const R123: u64 = // 2602880
        TOTAL_CASES / 2
            - LOW_RETURN_RATIO[5] * LOTTERY_CASES[5]
            - LOW_RETURN_RATIO[4] * LOTTERY_CASES[4];
    match rank {
        1..=3 => R123 as f64 * HIGH_RETURN_RATIO[rank] / LOTTERY_CASES[rank] as f64,
        4..=5 => LOW_RETURN_RATIO[rank] as f64,
        _ => 0.0,
    }
}

Covering design problem

저는 그 어떤 경우에도 항상 5등 당첨이 보장되도록 로또를 구매하는 경우의 수를 구하고 싶었습니다. 하지만 아이디어가 좀처럼 떠오르지 않아 인터넷과 GPT를 사용해서 이런저런 것들을 알아보았고 covering design이라는 수학 문제와, 여러 케이스에 대해 covering design의 해를 저장하는 La Jolla Covering Repository라는 것을 알게 되었습니다.

Covering design problem은 NP-hard입니다. 그래서 임의의 \(n\), \(k\), 그리고 \(t\)에 대해 \(C(n, k, t)\)를 빠르게 구하는 법은 알려져 있지 않습니다. 로또의 경우, \(728 \le C(45, 6, 3) \le 840\) 이라는 사실이 알려져있으며, 이 링크에서 820개의 블럭을 사용한 해가 나와있습니다. 위 링크에 나온 대로 820개의 로또를 구매하면, 최소 1장 이상의 5등 이상 당첨을 보장할 수 있습니다.

저의 기대는 이런 식으로 "커스텀한 분포를 사용하여(번호는 매 로또 회차마다 random mapping) 로또 당첨 기댓값을 조금이라도 끌어올릴 수 있지 않을까?" 였습니다. 후술하겠지만 이것은 그저 variance에 변화가 있을 뿐이며, expectation은 전혀 변하지 않는 방법이었습니다. 지금 생각해보면 참 부질없는데 당시에는 왜 이렇게 생각했지? 싶네요.

Rust programming

결론과 별개로 중간에 Rust 프로그래밍 언어를 사용하여 코딩을 진행했습니다. 로또 번호로 가능한 경우의 수(6개의 당첨번호 + 보너스번호)는 \(\binom{45}{6} \times (45 - 6) = 317657340\) 가지이므로, 해당 820개의 블럭을 317M개의 모든 로또번호에 대해서 전부 리턴을 일일이 계산하여 분포를 만들어내는 것은 Python 같은 언어로 코딩했을 때 매우 빡센 프로그램 실행시간이 나올 것으로 예상되었습니다.

그래서 rayon crate를 사용하여 parellel한 연산도 시도하고.. 별 짓을 다 했는데 결론은 그렇게 했음에도 불구하고 실행시간을 사람이 체감할 정도로 줄이는 것은 역부족이었다는 것이었습니다. 아마 제가 작은 vector를 연산 과정에서 엄청나게 많이 만든 것과 작은 연산들을 좀 큰 batch 단위로 묶지 않았던 것이 bottleneck이 되었을 것 같은데 (지나치게 작은 연산 덩어리들을 너무 많이 만들어내면 context switching 비용이 지나치게 커지기 때문), 이런 부분까지 줄인다면 꽤 괜찮은 실행 성능을 만들어낼 수 있을 것 같습니다.

Why is this meaningless?

그래서, 왜 이게 의미가 없는 지를 설명해드리겠습니다. 프로그램 실행성능이 한참 오래 걸려서, 모든 로또번호에 대해 820-block의 당첨금액을 시뮬레이션하지 않고 각 block에 대해 이 block을 당첨시킬 수 있는 로또번호에 대해서만 계산하기로 했습니다. 여기서 바로 "아차" 싶었습니다. 이 "아차"를 수학적으로 서술해드리면, 다음과 같습니다.

  • \(L\)을 가능한 모든 로또 번호의 집합이라고 정의합니다. \(L_i\)는 \(i\)번째 로또 번호입니다.
  • \(B\)를 제가 로또를 시도할 블럭의 집합이라고 정의합니다. \(B_i\)는 \(i\)번째 블럭입니다.
  • \(R(i, j)\)을 \(i\)번째 로또 번호가 걸렸을 때 \(j\)번째 블럭의 return이라고 정의합니다.
  • \(E\)를 1개 로또번호를 살 때 return의 기대값이라고 정의합니다. \(E = \frac{1}{2}\)입니다. 전체 로또 구매금의 50%를 당첨금으로 뿌리기 때문입니다.

그러면 어떤 로또 번호 \(L_i\)와 블럭 \(B\)에 대해 해당 블럭의 return은 다음과 같습니다.

\[\sum_{j} \frac{R(i, j)}{|B|}\]

그리고 제가 구하려던 것은 다음과 같습니다.

\[ \begin{align} \sum_{i \in L} \frac{\sum_{j \in B} \frac{R(i, j)}{|B|}}{|L|} &= \sum_{i \in L} \sum_{j \in B} R(i, j) \frac{1}{|B| |L|} \\ &= \sum_{j \in B} \sum_{i \in L} \frac{R(i, j)}{|L|} \frac{1}{|B|} \\ &= \sum_{j \in B} E \frac{1}{|B|} \\ &= E = 0.5 \end{align} \]

그래서 \(B\)가 어떤 식으로 구성되어 있더라도, 로또번호를 구매하는 행위는 기대값을 증가시키지 않습니다. 다만 covering problem의 해를 사용하여 구매를 하면 최소 1장 이상의 5등 이상의 당첨이 보장되므로(같은 수의 무작위의 복권을 구매하면 당첨이 1장도 안 되는 운 없는 경우가 존재함), variance는 다소 줄어들 수 있다고 볼 수 있겠습니다. 하지만 expectation은 그대로이므로, 그저 많은 양의 복권을 구매한만큼 빠르게 돈을 잃을 뿐입니다.

이상으로 저의 로또에 관한 뻘짓을 서술해보았습니다. 글을 읽어주셔서 감사합니다.